Practice Problems

1. $\mathrm{A}(\mathrm{x})=\int_{0}^{x} 3 t^{2} \mathrm{dt}$

(a) Use part 2 of the Fundamental Theorem to find a formula for $\mathrm{A}(x)$ and then differentiate $\mathrm{A}(x)$ to obtain a formula for $\mathrm{A}^{\prime}(x)$. Evaluate $\mathrm{A}^{\prime}(x)$ at $x=1,2$ and $3$.

(b) Use part 1 of the Fundamental Theorem to evaluate $\mathrm{A}^{\prime}(x)$ at $x=1,2,$ and $3$.

In problems 3 – 7 , evaluate $\mathrm{A}^{\prime}(x)$ at $x=1,2,$ and $3$.

3. $\mathrm{A}(\mathrm{x})=\int_{0}^{x} 2 t \mathrm{dt}$

5. $\mathrm{A}(\mathrm{x})=\int_{-3}^{x} 2 t \mathrm{dt}$

7. $\mathrm{A}(\mathrm{x})=\int_{0}^{x} \sin (t) \mathrm{dt}$

In problems 9 – 11 $\mathrm{A}(x)=\int_{0}^{x} \mathrm{f}(t)$ for the functions in Figures 10 – 14. Evaluate $\mathrm{A}^{\prime}(1), \mathrm{A}^{\prime}(2), \mathrm{A}^{\prime}(3)$.

9. $f$ in Fig. 10

11. $f$ in Fig. 12

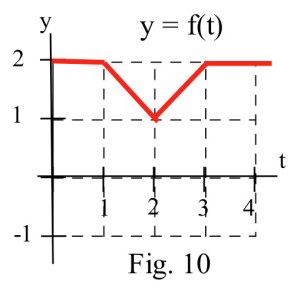
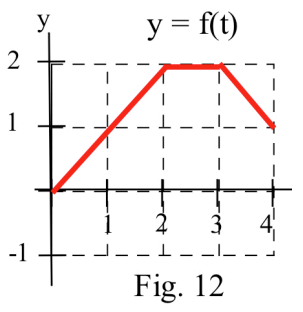
In problems 13 – 33, verify that $\mathrm{F}(x)$ is an antiderivative of the integrand $\mathrm{f}(x)$ and use Part 2 of the Fundamental Theorem to evaluate the definite integrals.

13. $\int_{0}^{1} 2 x \mathrm{dx}, \mathrm{F}(x)=x^{2}+5$

15. $\int_{1}^{3} x^{2} \mathrm{dx}, \mathrm{F}(x)=\frac{1}{3} x^{3}$

17. $\int_{1}^{5} \frac{1}{x} \mathrm{dx}, \mathrm{F}(x)=\ln (x)$

19. $\int_{1 / 2}^{3} \frac{1}{x} \mathrm{dx}, \mathrm{F}(x)=\ln (x)$

21. $\int_{0}^{\pi / 2} \cos (x) \mathrm{dx}, \mathrm{F}(x)=\sin (x)$

23. $\int_{0}^{1} \sqrt{x} \mathrm{dx}, \mathrm{F}(x)=\frac{2}{3} x^{3 / 2}$

25. $\int_{1}^{7} \sqrt{x} \mathrm{dx}, \mathrm{F}(x)=\frac{2}{3} x^{3 / 2}$

27. $\int_{1}^{9} \frac{1}{2 \sqrt{x}} \mathrm{dx}, \mathrm{F}(x)=\sqrt{x}$

29. $\int_{-2}^{3} \mathrm{e}^{x} \mathrm{dx}, \mathrm{F}(x)=\mathrm{e}^{x}$

31. $\int_{0}^{\pi / 4} \sec ^{2}(x) \mathrm{dx}, \mathrm{F}(\mathrm{x})=\tan (x)$

33. $\int_{0}^{3} 2 x \sqrt{1+x^{2}} \mathrm{dx}, \mathrm{F}(\mathrm{x})=\frac{2}{3}\left(1+x^{2}\right)^{3 / 2}$

For problems 33 – 47, find an antiderivative of the integrand and use Part 2 of the Fundamental Theorem to evaluate the definite integral.

35. $\int_{-1}^{2} x^{2} d x$

37. $\int_{1}^{\mathrm{e}} \frac{1}{x} \mathrm{dx}$

39. $\int_{25}^{100} \sqrt{x} \mathrm{dx}$

41. $\int_{1}^{10} \frac{1}{x^{2}} d x$

43. $\int_{0}^{1} e^{x} d x$

45. $\int_{\pi / 6}^{\pi / 4} \sec ^{2}(x) d x$

47. $\int_{3}^{3} \sin (x) \cdot \ln (x) d x$

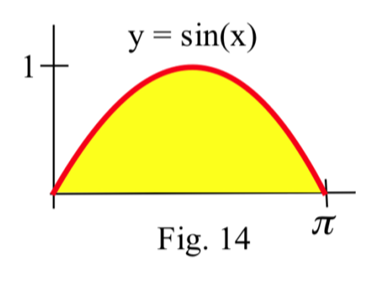
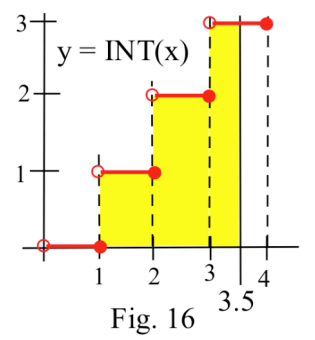
In problems 49 – 53 , find the area of each shaded region.

49. Region in Fig. 14

51. Region in Fig. 16.

53. Region in Fig. 18.

Leibniz' Rule

55. If $\mathbf{D}(A(x))=\tan (x)$, then find $\mathbf{D}(\mathrm{A}(3 x)), \mathbf{D}\left(\mathrm{A}\left(x^{2}\right)\right)$ and $\mathbf{D}(\mathrm{A}(\sin (x)))$.

57. $\frac{\mathrm{d}}{\mathrm{dx}}\left(\int_{1}^{5 x} \sqrt{1+t} \mathrm{dt}\right)$

59. $\frac{\mathrm{d}}{\mathrm{dx}}\left(\int_{0}^{\sin (x)} \sqrt{1+t} \mathrm{dt}\right.$

61. $\frac{\mathrm{d}}{\mathrm{dx}}\left(\int_{0}^{1-2 x} 3 t^{2}+2 \mathrm{dt}\right)$

63. $\frac{\mathrm{d}}{\mathrm{dx}}\left(\int_{x}^{\pi} \cos (3 t) \mathrm{dt}\right)$

65. $\frac{\mathrm{d}}{\mathrm{d} \mathrm{x}}\left(\int_{x}^{x^{2}} \tan (t) \mathrm{dt}\right)$

67. $\frac{\mathrm{d}}{\mathrm{dx}}\left(\int_{2}^{\ln (x)} 5 t \cos (3 t) \mathrm{dt}\right)$

Source: Dale Hoffman, https://learn.saylor.org/pluginfile.php/1403575/mod_resource/content/2/CC_4_5_FundamentalThm.pdf
This work is licensed under a Creative Commons Attribution 3.0 License.

1.

(a) $A(x)=x^{3}$. Then $A^{\prime}(x)=3 x^{2}$, and $\mathrm{A}^{\prime}(1)=3, \mathrm{~A}^{\prime}(2)=12$, and $A^{\prime}(3)=27$

(b) $\begin{gathered} \mathrm{A}^{\prime}(\mathrm{x})=\mathrm{D}\left(\int_{0}^{\mathrm{x}} 3 \mathrm{t}^{2} \mathrm{dt}\right)=3 \mathrm{x}^{2} \cdot \mathrm{A}^{\prime}(1)=3, \mathrm{~A}^{\prime}(2)=12, \text { and } \mathrm{A}^{\prime}(3)=27 \\\end{gathered}$

3. $A^{\prime}(x)=2 x \text { so } A^{\prime}(1)=2, A^{\prime}(2)=4, A^{\prime}(3)=6$

5. $A^{\prime}(x)=2 x \text { so } A^{\prime}(1)=2, A^{\prime}(2)=4, A^{\prime}(3)=6$

7. $\mathrm{A}^{\prime}(\mathrm{x})=\sin (\mathrm{x}) \text { so } \mathrm{A}^{\prime}(1) \approx 0.84, \mathrm{~A}^{\prime}(2) \approx 0.91, \mathrm{~A}^{\prime}(3) \approx 0.14$

9. $A^{\prime}(x)=f(x) \text { so } A^{\prime}(1)=2, A^{\prime}(2)=1, A^{\prime}(3)=2$

11. $A^{\prime}(x)=f(x) \text { so } A^{\prime}(1)=1, A^{\prime}(2)=2, A^{\prime}(3)=2$

13. $F(1)-F(0)=6-5=1$

15. $\mathrm{F}(3)-\mathrm{F}(1)=9-\frac{1}{3}=\frac{26}{3}$

17. $F(5)-F(1) \approx 1.61-0=1.61$

19. $\mathrm{F}(3)-\mathrm{F}(1 / 2) \approx 1.10-(-0.69)=1.79$

21. $\mathrm{F}(\pi / 2)-\mathrm{F}(0)=1-0=1$

23. $F(1)-F(0) \approx 0.67-0=0.67$

25. $\mathrm{F}(7)-\mathrm{F}(1)=\frac{2}{3}(7)^{3 / 2}-\frac{2}{3} \approx 11.68$

27. $\mathrm{F}(9)-\mathrm{F}(1)=3-1=2$

29. $\mathrm{F}(3)-\mathrm{F}(-2) \approx 20.09-0.14=19.95$

31. $\mathrm{F}(\pi / 4)-\mathrm{F}(0)=1-0=1$

33. $\mathrm{F}(3)-\mathrm{F}(0)=\frac{2}{3}(10)^{3 / 2}-\frac{2}{3} \approx 20.42$

35. $\mathrm{F}(\mathrm{x})=\frac{1}{3} \mathrm{x}^{3} \cdot \mathrm{F}(2)-\mathrm{F}(-1)=\frac{8}{3}-\left(-\frac{1}{3}\right)=3$

37. $F(x)=\ln (x) . F(e)-F(1)=1-0=1$

39. $\mathrm{F}(\mathrm{x})=\frac{2}{3} \mathrm{x}^{3 / 2} \cdot \mathrm{F}(100)-\mathrm{F}(25)=\frac{2000}{3}-\frac{250}{3}=\frac{1750}{3} \approx 583.33$

41. $\mathrm{F}(\mathrm{x})=-1 / \mathrm{x} . \mathrm{F}(10)-\mathrm{F}(1)=-0.1-(-1)=0.9$

43. $\mathrm{F}(\mathrm{x})=\mathrm{e}^{\mathrm{x}} \cdot \mathrm{F}(1)-\mathrm{F}(0)=\mathrm{e}-1 \approx 1.718$

45. $\mathrm{F}(\mathrm{x})=\tan (\mathrm{x}) . \mathrm{F}(\pi / 4)-\mathrm{F}(\pi / 6) \approx 1-0.577=0.423$

47. The integral goes from 3 to 3 so even without knowing an antiderivative, $\int_{3}^{3} \sin (x) \cdot \ln (x) d x=0$.

49. $\text { area }=\int_{0}^{\pi} \sin (x) d x=-\left.\cos (x)\right|_{0} ^{\pi}=-(-1)-(-1)=2$.

51. $\text { area } \left.=\int_{0}^{3.5} \operatorname{INT}(x) d x\right)=0+1+2+\frac{1}{2}(3)=4.5 \text {. }$

53. $\text { area }=\int_{0}^{3}(x-2)^{2} \mathrm{dx}=\int_{0}^{3} \mathrm{x}^{2}-4 \mathrm{x}+4 \mathrm{dx}=\frac{1}{3} \mathrm{x}^{3}-2 \mathrm{x}^{2}+\left.4 \mathrm{x}\right|_{0} ^{3}=3-0=3 .$

55. $\mathbf{D}(\mathrm{A}(3 \mathrm{x}))=\mathbf{3} \cdot \tan (3 \mathrm{x}), \mathbf{D}\left(\mathrm{A}\left(\mathrm{x}^{2}\right)\right)=2 \mathbf{x} \cdot \tan \left(\mathrm{x}^{2}\right), \mathbf{D}(\mathrm{A}(\sin (\mathrm{x})))=\cos (\mathbf{x}) \cdot \tan (\sin (\mathrm{x}))$

57. $\sqrt{1+5 x} \cdot (5)$

59. $\sqrt{1+\sin (x)} \cdot \cos (x)$

61. $\left\{3(1-2 x)^{2}+2\right\} \cdot(-2)$

63. $-\cos (3 x)$

65. $\tan \left(x^{2}\right) \cdot 2 x-\tan (x)$

67. $5 \cdot \ln (x) \cdot \cos (3 \cdot \ln (x)) \cdot \frac{1}{x}$